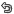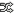2002. 4. 23
1. For given 2 lines
Show that the angle @ between two lines
2. Find the intersection point between the plane 3x+4y+z=24 and the line whose end points are p0=(10,-10,2), p1=(10,2,2)
| y1 = m1x1 - b1 |
| y2 = m2x1 - b2 |
Show that the angle @ between two lines
| tan@ = (m1-m2) / (1+m1*m2) |
2. Find the intersection point between the plane 3x+4y+z=24 and the line whose end points are p0=(10,-10,2), p1=(10,2,2)
(a) First. find the parametric equation for line for (t = 0 ~ 1)
(b) Find the value of the parametric variable corresponding to the intersection point.
(c) Find the values of the X,Y,Z coordinate values of plane.
(b) Find the value of the parametric variable corresponding to the intersection point.
(c) Find the values of the X,Y,Z coordinate values of plane.
(a) Compute the scalar product.
(b) Compute the angle between the vectors.
(b) Compute the angle between the vectors.
4.
(a) pivoting 방법을 선택하는 이유를 설명하시오.
(b) Maximal column pivoting 과
(c) Scaled partial pivoting 개념을 설명하시오.
(b) Maximal column pivoting 과
(c) Scaled partial pivoting 개념을 설명하시오.
5. Lagrange, Hermite, spline 함수의 특징을 Smoothness 관점에서 비교 설명하시오.
6. For given p0, p1, p0u, p1u, induce the p(u)=au^3 + bu^2 + cu + d, in the form of p(u)=U*M*B (여기서는 Dot Product임)
where
~cpp U = [u^3 u^2 u 1] B = [p0 p1 p0u, p1u ]T M = [ 2 2 1 1 ] [ -3 3 -2 -1 ] [ 0 0 1 0 ] [ 1 0 0 0 ]