Difference between r1.5 and the current
@@ -19,8 +19,9 @@
* 외적(cross product)
두 벡터의 수직인 벡터가 결과 값으로 나옴. (두 가지의 경우가 나옴)
attachment:484px-Cross_product_vector.svg.png
V는 우리가 보고 있는 방향
W는 우리가 돌리고 싶은 방향
W의 방향으로 돌리고 싶으면 V × W을 계산하면 된다.
V × W 가 음수라면 시계 방향 회전
V × W 가 양수라면 반시계 방향 회전이다.
두 벡터의 수직인 벡터가 결과 값으로 나옴. (두 가지의 경우가 나옴)
attachment:484px-Cross_product_vector.svg.png
A는 우리가 보고 있는 방향
B는 우리가 돌리고 싶은 방향
B의 방향으로 돌리고 싶으면 A × B을 계산하면 된다.
A × B 가 음수라면 시계 방향 회전
A × B 가 양수라면 반시계 방향 회전이다.
* 이와 같이 벡터의 내적과 외적을 이용해서 나아갈 방향을 알 수 있다.
1. 벡터의 원리 ¶
- 이동, 속도, 가속 등의 양을 나타내는데 사용된다.
- 2D에서는 (x, y) 3D에서는 (x, y, z)
- 벡터의 길이(크기)
│V│ = root(x^2 + y^2)
- 정규화(Normalizing)
벡터의 길이가 1이 되도록 크기를 조정. 방향은 일정하다.
정규화 된 벡터를 단위 벡터(Unit vector)라고 한다.
- 내적(dot product)
V·W = Vx × Wx + Vy × Wy
내적의 의미
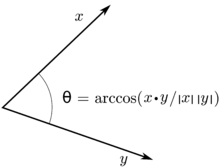[PNG image (5.68 KB)]
내적이 0보다 크면 두 벡터가 이루는 각도는 90도 이하이다.(예각이다)
내적이 0보다 작으면 두 벡터가 이루는 각도는 90도 이상이다.(둔각이다)
arcos를 이용해서 각도를 구할 수 있다.
단 이 각도가 양의 각도인지 음의 각도인지 알 수가 없다.
- 외적(cross product)
두 벡터의 수직인 벡터가 결과 값으로 나옴. (두 가지의 경우가 나옴)
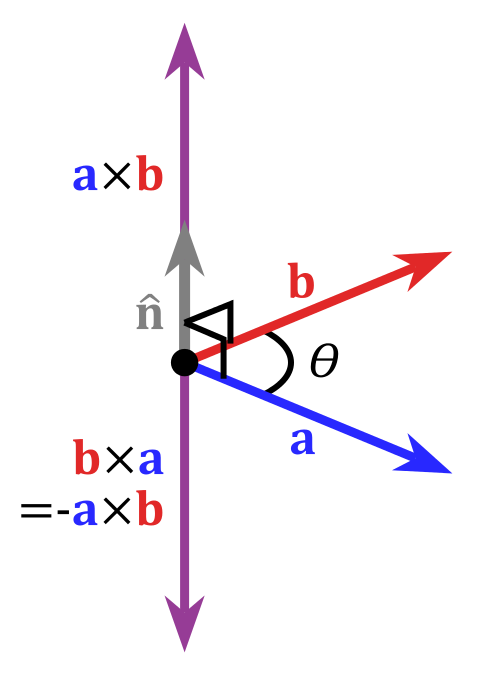[PNG image (26.79 KB)]
A는 우리가 보고 있는 방향
B는 우리가 돌리고 싶은 방향
B의 방향으로 돌리고 싶으면 A × B을 계산하면 된다.
A × B 가 음수라면 시계 방향 회전
A × B 가 양수라면 반시계 방향 회전이다.
- 이와 같이 벡터의 내적과 외적을 이용해서 나아갈 방향을 알 수 있다.
