3.1. Priority Queue ¶
- In computer science/data structures, a priority queue is an abstract data type which is like a regular queue or stack data structure, but where additionally each element has a "priority" associated with it. In a priority queue, an element with high priority is served before an element with low priority. If two elements have the same priority, they are served according to their order in the queue.
- While priority queues are often implemented with heaps, they are conceptually distinct from heaps. A priority queue is an abstract concept like "a list" or "a map"; just as a list can be implemented with a linked list or an array, a priority queue can be implemented with a heap or a variety of other methods such as an unordered array.
- 출처 : http://en.wikipedia.org/wiki/Priority_queue
3.2. Priority Queue in STL ¶
#include<iostream>
#include<cstdlib>
#include<ctime>
#include<queue>
using namespace std;
priority_queue <int> pq;
int v[100];
int main(void)
{
int n = 10;
srand(time(NULL));
printf("Vector \n");
for(int i = 0; i<n; i++){
v[i] = rand() % 100;
printf("%d ", v[i]);
}
printf("\n\n");
for(int i = 0; i<n; i++){
pq.push(v[i]);
}
printf("Priority Queue \n");
while(!pq.empty()){
printf("%d ", pq.top());
pq.pop();
}
printf("\n\n");
}
3.3. Heap ¶
- 힙(Heap)은 특별한 트리를 기본으로 한 자료구조(tree-based structure)로서 다음과 같은 heap 속성(property)을 만족한다.
- A가 B의 부모노드(parent node) 이면, 힙(heap) 에 적용된 것과 같은 순서로 key(B)에 관해서 key(A)는 순서가 정해진다.
- 각 노드의 children 의 최대개수는 heap 의 종류에 따라 다르지만, 많은 타입에서 children 의 개수는 2개 이하이다. 그리고 이것은 이진 힙(binary heap)으로 알려져 있다.
- 출처 : http://ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
- Heap Visualization - http://www.cs.usfca.edu/~galles/visualization/Heap.html
- A heap data structure should not be confused with the heap which is a common name for the pool of memory from which dynamically allocated memory is allocated. The term was originally used only for the data structure.
3.4.1. Property ¶
- Shape property
The tree is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
- Heap property
All nodes are either greater than or equal to or less than or equal to each of its children, according to a comparison predicate defined for the heap.
3.5. Heap Sort ¶
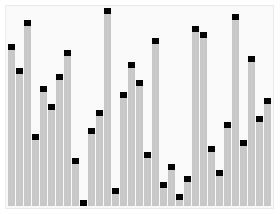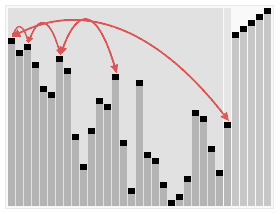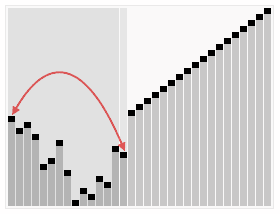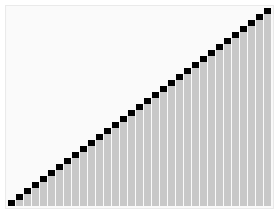
[GIF image (274.43 KB)]
- 간단한 설명 : http://ko.wikipedia.org/wiki/%ED%9E%99_%EC%A0%95%EB%A0%AC
- Heap Sort Visualization - http://www.cs.usfca.edu/~galles/visualization/HeapSort.html
3.6. Application of Priority Queue ¶
- Dijkstra's algorithm : 최단 경로를 구하는 알고리즘인데 그래프 시간에 배웁니다.
- http://en.wikipedia.org/wiki/Dijkstra%27s_algorithm#Using_a_priority_queue
- Best-first search algorithms
- Prim's algorithms










