3.1. Priority Queue ¶
- In computer science/data structures, a priority queue is an abstract data type which is like a regular queue or stack data structure, but where additionally each element has a "priority" associated with it. In a priority queue, an element with high priority is served before an element with low priority. If two elements have the same priority, they are served according to their order in the queue.
- While priority queues are often implemented with heaps, they are conceptually distinct from heaps. A priority queue is an abstract concept like "a list" or "a map"; just as a list can be implemented with a linked list or an array, a priority queue can be implemented with a heap or a variety of other methods such as an unordered array.
- 출처 : http://en.wikipedia.org/wiki/Priority_queue
3.2. Priority Queue in STL ¶
#include<iostream>
#include<cstdlib>
#include<ctime>
#include<queue>
using namespace std;
priority_queue <int> pq;
int v[100];
int main(void)
{
int n = 10;
srand(time(NULL));
printf("Vector \n");
for(int i = 0; i<n; i++){
v[i] = rand() % 100;
printf("%d ", v[i]);
}
printf("\n\n");
for(int i = 0; i<n; i++){
pq.push(v[i]);
}
printf("Priority Queue \n");
while(!pq.empty()){
printf("%d ", pq.top());
pq.pop();
}
printf("\n\n");
}
3.3. Heap ¶
- 힙(Heap)은 특별한 트리를 기본으로 한 자료구조(tree-based structure)로서 다음과 같은 heap 속성(property)을 만족한다.
- A가 B의 부모노드(parent node) 이면, 힙(heap) 에 적용된 것과 같은 순서로 key(B)에 관해서 key(A)는 순서가 정해진다.
- 각 노드의 children 의 최대개수는 heap 의 종류에 따라 다르지만, 많은 타입에서 children 의 개수는 2개 이하이다. 그리고 이것은 이진 힙(binary heap)으로 알려져 있다.
- 출처 : http://ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
- Heap Visualization - http://www.cs.usfca.edu/~galles/visualization/Heap.html
- A heap data structure should not be confused with the heap which is a common name for the pool of memory from which dynamically allocated memory is allocated. The term was originally used only for the data structure.
3.4.1. Property ¶
- Shape property
The tree is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
- Heap property
All nodes are either greater than or equal to or less than or equal to each of its children, according to a comparison predicate defined for the heap.
3.4.2. Operation ¶
- Max Heap 이라고 가정하자.
- 삽입
- 가장 마지막 위치에 원소를 삽입한다.
- 삽입 한 원소를 원소의 부모와 비교한다. 만약 부모가 더 크다면 멈춘다.
- 부모가 더 작다면, 부모와 위치를 바꾼다. 그리고 다시 그 위치에서 부모와 비교...
- 가장 마지막 위치에 원소를 삽입한다.
- 삭제
- Root의 원소를 제거하고, Root에 Heap에 가장 마지막 위치에 있는 원소를 놓는다.
- 새로운 Root와 Root의 자식과 비교한다. 만약 Root가 더 크다면 멈춘다.
- Root가 더 작다면, 자식과 위치를 교체한다. 그리고 다시 그 위치에서 자식과 비교...
- Root의 원소를 제거하고, Root에 Heap에 가장 마지막 위치에 있는 원소를 놓는다.
3.5. Heap Sort ¶
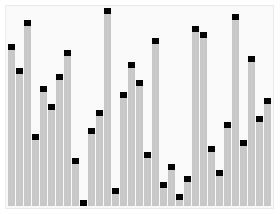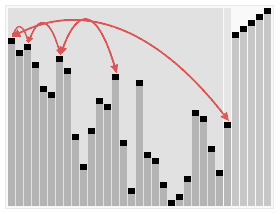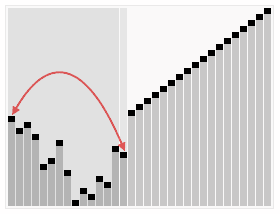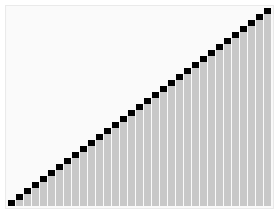
[GIF image (274.43 KB)]
- 간단한 설명 : http://ko.wikipedia.org/wiki/%ED%9E%99_%EC%A0%95%EB%A0%AC
- Heap Sort Visualization - http://www.cs.usfca.edu/~galles/visualization/HeapSort.html
3.6. Application of Priority Queue ¶
- Dijkstra's algorithm : 최단 경로를 구하는 알고리즘인데 그래프 시간에 배웁니다.
- http://en.wikipedia.org/wiki/Dijkstra%27s_algorithm#Using_a_priority_queue
- Best-first search algorithms
- Prim's algorithms
- 그 외에도 여러가지 등등등..
4. 후기 ¶
- 주제를 하나를 잡고 설명하려니까 편하네요. 피드백을 받아서 개선을 해보려고 하는데 개선이 되는지는 잘 못느끼겠네요. 좀 더 피드백을 주었으면 합니다. 더 좋은 새싹 교실이 될 수 있도록 하고 싶네요. 강사나 학생에게나 시간 낭비가 되지 않는 새싹이 되었으면 합니다. 다음 주는 Map과 Binary Search Tree를 가르칠 계획입니다. Floyd Algorithm까지는 갈 길이 머네요. 올 해가 가기 전에는 마무리 해야 될텐데... - 권영기
- 뭔가 늘어납니다! 재귀만 보면 머리가 아파오는 저가 이걸 제대로 따라갈수 있을지 걱정입니다. 넘어아 할 사이니 이번기회에 극복해보는걸로, 쿨럭
- 이번에 참고자료가 더 많아져서 설명도 알아듣기 편했고, 주제도 한가지라 생각이 집중되서 괜찮다는 생각이 들었습니다. (특히 눈에 보이는 예시를 보면 확실히 이해가 빠르네요) 영기형이 시간을 더 투자해주시는 만큼 더 좋은 새싹이 되가는 것 같습니다.
감사히 잘 받아먹겠습니다.지금까지 새싹교실 하면서 정말 재밌게 들었는데, 이번 시간은 더 재밌게 들었네요. 뭔가 개선했으면 좋을 거 같은게 생각나면 남길텐데, 딱히 생각이 안나네요. 생각나면 위키나 카톡으로 전해드리겠습니다. - 김정민
5.1. 김정민 ¶
- node의 개수가 31개로 고정적인 Binary Heap을 배열을 이용해서 구현해봤습니다. 크기가 한정적이라 영기형이 조언해준대로 포인터를 이용한 방법으로도 만들어 봐야겠네요. 기능은 push(insert)와 pop(delete)만 있습니다.
- Min Heap입니다.
- index가 0이 아닌 1부터 시작하는걸 잊고 뻘짓을 좀 했습니다.
- pop할 때,
ppt안보고아래에서 올라가는 방법을 사용하다가 그러면 complete tree가 안된다는걸 깨닫고게다가 pop자체도 제대로 안됨다시 제대로 짰습니다.
#include <stdio.h>
// min이 가장 위에 가도록!
int heap[32]; //동적할당, 포인터로 바꿔보자 ㅠㅠ
//실제 data가 들어가는 index는 0부터가 아니라 1부터임!
int push(int num){
int i;
for (i = 1; i < 32; i++){
if (heap[i] == -1){ //이거 때문에 일단 양의 정수만 넣을수 있음 (count를 쓰는 방법도 있지만 이걸로 해봄)
heap[i] = num;
break;
}
if (i == 31){
printf("the heap is full\n");
return 1;
}
}
while(heap[i] < heap[i / 2]){
int temp_for_change;
temp_for_change = heap[i];
heap[i] = heap[i / 2];
heap[i / 2] = temp_for_change;
i = i / 2;
}
}
int pop(){
int last_num_index; //숫자가 있는 마지막 칸의 index
int j=1, small_num_index; //for 'while'
for (int i = 1; i < 32; i++){
if (heap[i] == -1){
if (i == 1){
printf("heap is empty\n");
return 1;
}
last_num_index = i - 1;
break;
}
if (i == 31){
last_num_index = 31;
}
}
heap[1] = heap[last_num_index];
heap[last_num_index] = -1;
while (1){
if ((heap[j] > heap[j * 2] && heap[j * 2] != -1) || (heap[j] > heap[j * 2 + 1] && heap[j*2+1] != -1)){ //children 중에 parent보다 작은놈이 있다!
int temp_for_change;
if (heap[j * 2] <= heap[j * 2 + 1] || heap[j*2+1] == -1){ //왼쪽을 끌어올린다
small_num_index = j * 2;
}
else{ //오른쪽을 끌어올린다
small_num_index = j * 2 + 1;
}
temp_for_change = heap[small_num_index];
heap[small_num_index] = heap[j];
heap[j] = temp_for_change;
j = small_num_index;
}
else{
return 0;
}
}
}
void view_top(){
printf("top : %d\n", heap[1]);
}
/*
void view_all(){ //just for debug
for (int i = 1; i < 32; i++){
printf("%d ", heap[i]);
}
printf("\n");
}
*/
void main(){
int temp;
int num;
for (int i = 0; i < 32; i++){
heap[i] = -1;
}
while (1){
printf("push : 1, pop : 2\tinput : ");
scanf_s("%d", &temp);
switch (temp){
case 1:
printf("num : ");
scanf_s("%d", &num);
push(num);
//view_all();
break;
case 2:
view_top();
pop();
//view_all();
break;
default:
break;
}
if (temp != 1 && temp != 2)
break;
}
}
5.2. 이지수 ¶
시간이 없어서 숫자를 입력받아 큰 수부터 작은 수까지 정렬하는 건 못했어요 ㅠㅠ암튼 재밌네용
참 저는 min heap인줄 모르고 max heap을 했습니다.
참 저는 min heap인줄 모르고 max heap을 했습니다.
#pragma warning(disable: 4996)
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define SIZE 50
void fillHeap(int* heap, int number_of_element);
void insert(int* heap, int i);
void delete(int* heap, int i, int number_of_element);
void swap(int* a, int* b);
void displayHeap(int* heap, int number_of_element);
int main(){
int* heap = (int *)malloc(SIZE*sizeof(int));
int number_of_element = 0;
int option = 0;
printf("type number of elements : ");
scanf("%d", &number_of_element);
fillHeap(heap, number_of_element);
while (1){
printf("Select(1. push 2. pop 3. show heap 4. exit) : ");
scanf("%d", &option);
switch (option){
case 1:
number_of_element++;
printf("Enter new element : ");
scanf("%d", heap + number_of_element);
insert(heap, number_of_element);
break;
case 2:
*(heap + 1) = *(heap + number_of_element);
number_of_element--;
delete(heap, 1, number_of_element);
break;
case 3:
displayHeap(heap, number_of_element);
break;
case 4:
printf("Program Ended.\n");
system("pause");
return 0;
break;
default:
printf("Wrong Number. \n");
break;
}
}
return 0;
}
void fillHeap(int* heap, int number_of_element){
int i = 0, element = 50;
for (i = 1; i <= number_of_element; i++){
*(heap + i) = element--;
}
}
void displayHeap(int* heap, int number_of_element){
int i = 0, exponent = 0;
for (i = 1; i <= number_of_element; i++){
if (i == pow(2, exponent)){
exponent++;
printf("\n");
}
printf("%d ", *(heap + i));
}
printf("\n");
}
void insert(int* heap, int i){
if (*(heap + i / 2) < *(heap + i)){
swap(heap + i / 2, heap + i);
}
if (i / 2 != 1){
insert(heap, i / 2);
}
}
void delete(int* heap, int i, int number_of_element){
if (*(heap + 2 * i) > *(heap + 2 * i + 1) && 2*i <= number_of_element){
swap(heap + i, heap + 2 * i);
delete(heap, 2 * i, number_of_element);
}
else if(*(heap + 2 * i) < *(heap + 2 * i + 1) && 2*i + i <= number_of_element) {
swap(heap + i, heap + 2 * i + 1);
delete(heap, 2 * i + 1, number_of_element);
}
}
void swap(int* a, int* b){
int temp = *a;
*a = *b;
*b = temp;
}










