Difference between r1.29 and the current
@@ -1,5 +1,6 @@
[[TableOfContents]]
* 우리나라 말로 선형 회귀
* 변수 하나만 쓰이면 단순 선형 회귀, 둘 이상의 변수가 쓰이면 다중 선형 회귀라고 함.
* 수식 정리를 어떻게 해야할지 모르겠음.. 첫 장부터 포기해야하는가..
* 수식 정리를 어떻게 해야할지 모르겠음.. 첫 장부터 포기해야하는가..
* 이 문서에 있는 사진이나 예제의 상당수는 [https://www.coursera.org/course/ml Coursera/ML강의]에 남겨져 있음. PPT도 제공하므로 꼭 확인하세요.
=== Linear Regression ===* 우리나라 말로 선형 회귀
* 변수 하나만 쓰이면 단순 선형 회귀, 둘 이상의 변수가 쓰이면 다중 선형 회귀라고 함.
@@ -28,5 +29,76 @@
attachment:CostFunctionGraph1.PNG
* 가장 아래에 있는 지점이 데이터 모델을 잘 표현하는 Parameter임.(Cost가 가장 작음)
attachment:ContourPlot.PNG
* 가장 아래에 있는 지점이 데이터 모델을 잘 표현하는 Parameter임.(Cost가 가장 작음)
attachment:ContourPlot.PNG
*
* 같은 색으로 연결된 선은 같은 Cost를 가지고 있다는 의미임.
=== Gradient descent === * 경사 하강법(gradient descent)은 최초 근사값(first-order) 발견용 최적화알고리즘이다. 기본 아이디어는 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복시키는 것이다.
* 최적화할 함수 attachment:gd1.png 에 대하여, 먼저 시작점 attachment:gd2.png 를 정한다. 현재 attachment:gd3.png 가 주어졌을 때, 그 다음으로 이동할 점인 attachment:gd4.png 은 다음과 같이 계산된다.
attachment:gd5.png
* 이때 attachment:gd7.png 는 이동할 거리를 조절하는 매개변수이다. attachment:gd7.png 가 너무 작으면 수렴 속도가 느리다. attachment:gd7.png 가 크면 수렴 값을 넘어가버려서 수렴에 실패할 수 있다. 따라서 적절하게 잡아주는 것이 중요.
* 이 알고리즘의 수렴 여부는 '''f의 성질과 attachment:gd7.png 의 선택에 따라 달라진다.''' 또한, 이 알고리즘은 '''지역 최적해로 수렴'''한다. 따라서 구한 값이 전역적인 최적해라는 것을 보장하지 않으며 '''시작점 attachment:gd8.png 의 선택'''에 따라서 달라진다. 이에 따라 다양한 시작점에 대해 여러 번 경사 하강법을 적용하여 그 중 가장 좋은 결과를 선택할 수도 있다.
* [http://ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95 출처]
attachment:GradientDescentGraph1.PNG
attachment:GradientDescentGraph2.PNG
* Gradient Descent를 이용해서 Parameter를 구해낼 경우, 다음과 같은 모습을 보여준다.
attachment:GradientDescentAlgorithm.PNG
* 각 Parameter는 동시에 갱신해야 한다.
* attachment:gd7.png 는 매 Parameter 갱신 때마다 수정할 필요가 없다. 기울기에 의해서 수렴하는 정도가 조절되기 때문이다.
=== Octave로 Linear Regression With One Variable 구현 ===
==== computeCost ====
{{{
function J = computeCost(X, y, theta)
% Initialize some useful values
m = length(y); % number of training examples
J = 0;
for i=1:m,
J = J + (X(i,:) * theta - y(i)) ^ 2;
end
J = J / (2 * m);
}}}
==== gradientDescent ====
{{{
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
m2 = length(theta); % number of theta
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
delta = 0;
temp = theta;
for iter2 = 1:m2
for iter1 = 1:m
delta = delta + (X(iter1, :) * theta - y(iter1)) * X(iter1, iter2);
end
delta = delta / m;
temp(iter2, 1) = temp(iter2, 1) - alpha * delta;
end
theta = temp;
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
}}}
----
[MachineLearning스터디]
- 수식 정리를 어떻게 해야할지 모르겠음.. 첫 장부터 포기해야하는가..
- 이 문서에 있는 사진이나 예제의 상당수는 Coursera/ML강의에 남겨져 있음. PPT도 제공하므로 꼭 확인하세요.
1. Linear Regression ¶
- 우리나라 말로 선형 회귀
- 변수 하나만 쓰이면 단순 선형 회귀, 둘 이상의 변수가 쓰이면 다중 선형 회귀라고 함.
- 만약 목표가 예측일 경우, 선형 회귀를 통해 y와 x로 이루어진 집합을 만들기 위한 예측 모델을 개발한다. 개발된 모델은 차후 y가 없는 x값이 입력되었을 때, 해당 x에 대한 y를 예측하기 위해 사용한다.
- 여러 x가 존재할 경우, y와 x 간의 관계를 수량화하여 어느 x가 y와 별로 관계가 없는지 알아낸다.
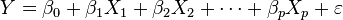 [PNG image (1.12 KB)]
[PNG image (1.12 KB)]
- 출처
2. Model Representation ¶
[PNG image (12.07 KB)]
- 예: 집 평수에 따른 가격
[PNG image (6.2 KB)]
- Training Set : 위의 기본 데이터 셋과 같음. 머신은 이런 데이터 셋을 기반으로 판단을 하게 됨.
- Learning Algorithm : Hypothesis(추정)를 만들어 냄.
- Hypothesis : 주어진 입력에 대한 출력을 추정해내는 함수를 말한다. h라고 많이 씀. 데이터 모델이 h와 같다고 추정하게 되면, 우리는 Training Set에 존재하지 않는 데이터에 대해서도 h를 통해서 값을 추정해낼 수 있다.
- 위의 예제는 변수가 하나만 쓰인 단순 선형 회귀임.
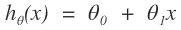 [PNG image (1.71 KB)]
[PNG image (1.71 KB)]
- θ를 Hypothesis의 Parameter라고 함.
- 중요한 것 : θ를 어떻게 결정할 것인가? -> Cost Function을 통해서 결정함.
3. Cost Function ¶
- 구해낸 Hypothesis가 데이터 모델을 잘 표현하고 있는지 평가하는 함수.
[PNG image (4.63 KB)]
- Cost Function에 의해서 가장 데이터 모델을 잘 표현하고 있다고 평가받는 Hypothesis를 구하는게 목표.
[PNG image (3.77 KB)]
- Cost Function을 시각화 했을 경우.
[PNG image (76.92 KB)]
- 가장 아래에 있는 지점이 데이터 모델을 잘 표현하는 Parameter임.(Cost가 가장 작음)
[PNG image (34.53 KB)]
- 같은 색으로 연결된 선은 같은 Cost를 가지고 있다는 의미임.
4. Gradient descent ¶
- 경사 하강법(gradient descent)은 최초 근사값(first-order) 발견용 최적화알고리즘이다. 기본 아이디어는 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복시키는 것이다.
- 최적화할 함수 에 대하여, 먼저 시작점
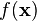 [PNG image (390 Bytes)]를 정한다. 현재
[PNG image (390 Bytes)]를 정한다. 현재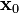 [PNG image (240 Bytes)]가 주어졌을 때, 그 다음으로 이동할 점인
[PNG image (240 Bytes)]가 주어졌을 때, 그 다음으로 이동할 점인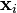 [PNG image (220 Bytes)]은 다음과 같이 계산된다.
[PNG image (220 Bytes)]은 다음과 같이 계산된다.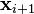 [PNG image (262 Bytes)]
[PNG image (262 Bytes)]
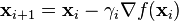
[PNG image (703 Bytes)]
- 이때 는 이동할 거리를 조절하는 매개변수이다.
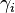 [PNG image (222 Bytes)]가 너무 작으면 수렴 속도가 느리다.
[PNG image (222 Bytes)]가 너무 작으면 수렴 속도가 느리다.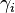 [PNG image (222 Bytes)]가 크면 수렴 값을 넘어가버려서 수렴에 실패할 수 있다. 따라서 적절하게 잡아주는 것이 중요.
[PNG image (222 Bytes)]가 크면 수렴 값을 넘어가버려서 수렴에 실패할 수 있다. 따라서 적절하게 잡아주는 것이 중요.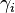 [PNG image (222 Bytes)]
[PNG image (222 Bytes)]
- 이 알고리즘의 수렴 여부는 f의 성질과 의 선택에 따라 달라진다. 또한, 이 알고리즘은 지역 최적해로 수렴한다. 따라서 구한 값이 전역적인 최적해라는 것을 보장하지 않으며 시작점
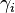 [PNG image (222 Bytes)]의 선택에 따라서 달라진다. 이에 따라 다양한 시작점에 대해 여러 번 경사 하강법을 적용하여 그 중 가장 좋은 결과를 선택할 수도 있다.
[PNG image (222 Bytes)]의 선택에 따라서 달라진다. 이에 따라 다양한 시작점에 대해 여러 번 경사 하강법을 적용하여 그 중 가장 좋은 결과를 선택할 수도 있다.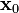 [PNG image (240 Bytes)]
[PNG image (240 Bytes)]
- 출처
[PNG image (123.66 KB)]
[PNG image (123.88 KB)]
- Gradient Descent를 이용해서 Parameter를 구해낼 경우, 다음과 같은 모습을 보여준다.
[PNG image (11.62 KB)]
- 각 Parameter는 동시에 갱신해야 한다.
- 는 매 Parameter 갱신 때마다 수정할 필요가 없다. 기울기에 의해서 수렴하는 정도가 조절되기 때문이다.
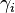 [PNG image (222 Bytes)]
[PNG image (222 Bytes)]
5.1. computeCost ¶
function J = computeCost(X, y, theta) % Initialize some useful values m = length(y); % number of training examples J = 0; for i=1:m, J = J + (X(i,:) * theta - y(i)) ^ 2; end J = J / (2 * m);
5.2. gradientDescent ¶
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
m2 = length(theta); % number of theta
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
delta = 0;
temp = theta;
for iter2 = 1:m2
for iter1 = 1:m
delta = delta + (X(iter1, :) * theta - y(iter1)) * X(iter1, iter2);
end
delta = delta / m;
temp(iter2, 1) = temp(iter2, 1) - alpha * delta;
end
theta = temp;
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end










