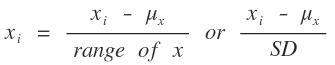MachineLearning스터디/LinearRegressionWithMultipleVariables (rev. 1.5)
2. Gradient Descent for Multiple Variables ¶
3. Feature Scaling ¶
[PNG image (3.12 KB)]
5. Polynomial Regression ¶
7. Octave로 Linear Regression With Multiple Varables 구현하기 ¶
7.1. Feature Normalize ¶
function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X
% FEATURENORMALIZE(X) returns a normalized version of X where
% the mean value of each feature is 0 and the standard deviation
% is 1. This is often a good preprocessing step to do when
% working with learning algorithms.
% You need to set these values correctly
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
n_of_feature = size(X_norm, 2);
for i = 1:n_of_feature
mu(i) = mean(X_norm(:, i));
sigma(i) = std(X_norm(:, i));
X_norm(:, i) = (X_norm(:, i ) - mu(i)) / sigma(i);
end
- mean : 평균 구하는 함수.
- std : 표준 편차 구하는 함수.
- 표준 편차를 이용해서 데이터를 정규화 시킴.
7.2. Compute Cost ¶
function J = computeCostMulti(X, y, theta)
%COMPUTECOSTMULTI Compute cost for linear regression with multiple variables
% J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
J = (X * theta - y)' * (X * theta - y) / (2 * m);
% =========================================================================
end
- 왜 이게 되는지는 모르겠음. 아는 사람은 추가바람.
7.3. Gradient Descent ¶
function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
%GRADIENTDESCENTMULTI Performs gradient descent to learn theta
% theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
temp = theta;
E = X * theta - y;
for j=1:size(X, 2)
delta = sum(E .* X(:, j)) / m;
temp(j, 1) = temp(j, 1) - alpha * delta;
end
theta = temp;
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCostMulti) and gradient here.
%
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCostMulti(X, y, theta);
end