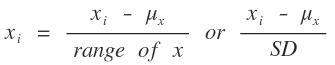Machine Learning스터디/Linear Regression With Multiple Variables

Difference between r1.3 and the current

@@ -1,11 +1,23 @@

[[TableOfContents]]

* 모든 것을 정리하려고 하니 효율이 떨어진다. 중요하다 생각되는 것만 우선 정리하기로..

* 이 문서에 있는 사진이나 예제의 상당수는 [https://www.coursera.org/course/ml Coursera/ML강의]에 남겨져 있음. PPT도 제공하므로 꼭 확인하세요.

=== Multiple Features ===
=== Gradient Descent for Multiple Variables ===

==== Cost Function ====

attachment:CostFunctionWithMultipleVariables.PNG

=== Feature Scaling ===

attachment:Mean_Normalization.png

=== Learning Rate ===
=== Polynomial Regression ===
=== Normal Equation ===

attachment:Normal_Equation.PNG

=== 정리 ===

==== Gradient Descent ====

* Learning Rate α를 잘 정하는게 중요.

* Feature의 수가 클 때 사용. (100000개 이상)

==== Normal Equation ====

* attachment:invert.png 의 계산이 필요. O(N^3)의 시간복잡도를 가짐.

* Feature의 수가 적을 때 사용. (10000개 까지)

=== Octave로 Linear Regression With Multiple Varables 구현하기 ===
==== Feature Normalize ====
{{{

@@ -27,7 +39,64 @@

X_norm(:, i) = (X_norm(:, i ) - mu(i)) / sigma(i);
end
}}}

* mean : 평균 구하는 함수.
* std : 표준 편차 구하는 함수.
* 표준 편차를 이용해서 데이터를 정규화 시킴.

==== Compute Cost ====

{{{

function J = computeCostMulti(X, y, theta)

%COMPUTECOSTMULTI Compute cost for linear regression with multiple variables

% J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the

% parameter for linear regression to fit the data points in X and y

% Initialize some useful values

m = length(y); % number of training examples

% You need to return the following variables correctly

J = 0;

% ====================== YOUR CODE HERE ======================

% Instructions: Compute the cost of a particular choice of theta

% You should set J to the cost.

J = (X * theta - y)' * (X * theta - y) / (2 * m);

% =========================================================================

end

}}}

* 왜 이게 되는지는 모르겠음. 아는 사람은 추가바람.

==== Gradient Descent ====

{{{

function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)

%GRADIENTDESCENTMULTI Performs gradient descent to learn theta

% theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by

% taking num_iters gradient steps with learning rate alpha

% Initialize some useful values

m = length(y); % number of training examples

J_history = zeros(num_iters, 1);

for iter = 1:num_iters

temp = theta;

E = X * theta - y;

for j=1:size(X, 2)

delta = sum(E .* X(:, j)) / m;

temp(j, 1) = temp(j, 1) - alpha * delta;

end

theta = temp;

% ====================== YOUR CODE HERE ======================

% Instructions: Perform a single gradient step on the parameter vector

% theta.

% Hint: While debugging, it can be useful to print out the values

% of the cost function (computeCostMulti) and gradient here.

% ============================================================

% Save the cost J in every iteration

J_history(iter) = computeCostMulti(X, y, theta);

end

}}}

----

[MachineLearning스터디]

1. Multiple Features

2. Gradient Descent for Multiple Variables

2.1. Cost Function

3. Feature Scaling

4. Learning Rate

5. Polynomial Regression

6. Normal Equation

7. 정리

7.1. Gradient Descent
7.2. Normal Equation

8. Octave로 Linear Regression With Multiple Varables 구현하기

8.1. Feature Normalize
8.2. Compute Cost
8.3. Gradient Descent

모든 것을 정리하려고 하니 효율이 떨어진다. 중요하다 생각되는 것만 우선 정리하기로..
이 문서에 있는 사진이나 예제의 상당수는 Coursera/ML강의에 남겨져 있음. PPT도 제공하므로 꼭 확인하세요.

1. Multiple Features ¶

2. Gradient Descent for Multiple Variables ¶

2.1. Cost Function ¶

[PNG image (5.24 KB)]

3. Feature Scaling ¶

[PNG image (3.12 KB)]

4. Learning Rate ¶

5. Polynomial Regression ¶

6. Normal Equation ¶

[PNG image (2.67 KB)]

7. 정리 ¶

7.1. Gradient Descent ¶

Learning Rate α를 잘 정하는게 중요.
Feature의 수가 클 때 사용. (100000개 이상)

7.2. Normal Equation ¶

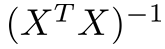[PNG image (2.74 KB)]
의 계산이 필요. O(N^3)의 시간복잡도를 가짐.
Feature의 수가 적을 때 사용. (10000개 까지)

8. Octave로 Linear Regression With Multiple Varables 구현하기 ¶

8.1. Feature Normalize ¶

function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X 
%   FEATURENORMALIZE(X) returns a normalized version of X where
%   the mean value of each feature is 0 and the standard deviation
%   is 1. This is often a good preprocessing step to do when
%   working with learning algorithms.

% You need to set these values correctly
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
n_of_feature = size(X_norm, 2);
for i = 1:n_of_feature
	mu(i) = mean(X_norm(:, i));
	sigma(i) = std(X_norm(:, i));
	X_norm(:, i) = (X_norm(:, i ) - mu(i)) / sigma(i);
end

mean : 평균 구하는 함수.
std : 표준 편차 구하는 함수.
표준 편차를 이용해서 데이터를 정규화 시킴.

8.2. Compute Cost ¶

function J = computeCostMulti(X, y, theta)
%COMPUTECOSTMULTI Compute cost for linear regression with multiple variables
%   J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.
J = (X * theta - y)' * (X * theta - y) / (2 * m);




% =========================================================================

end

왜 이게 되는지는 모르겠음. 아는 사람은 추가바람.

8.3. Gradient Descent ¶

function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
%GRADIENTDESCENTMULTI Performs gradient descent to learn theta
%   theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by
%   taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
	temp = theta;
	E = X * theta - y;
	for j=1:size(X, 2)
		delta = sum(E .* X(:, j)) / m;
		temp(j, 1) = temp(j, 1) - alpha * delta;
	end
	theta = temp;
    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCostMulti) and gradient here.
    %
    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCostMulti(X, y, theta);
end

MachineLearning스터디