Difference between r1.4 and the current
@@ -12,10 +12,10 @@
= 테스트 =
== Binary Search ==
''문제''
binary search(이진 탐색)는 이미 정렬된 배열을 대상으로 수행하는 검색 알고리즘이다.
첫 번째 과제는 오름차순으로 정렬된 정숫값을 가지는 1차원 배열로부터 원하는 값의 존재유무와 인덱스 번호를 출력하는 binary_search 함수를 구현하는 것이다.
만약 찾으려는 값이 배열에 존재하지 않으면 ''-1을 리턴''한다.
'''문제'''
binary search(이진 탐색)는 '''이미 정렬된 배열'''을 대상으로 수행하는 검색 알고리즘이다.
첫 번째 과제는 오름차순으로 정렬된 정숫값을 가지는 1차원 배열로부터 원하는 값의 존재유무를 검색하여 인덱스 번호를 출력하는 binary_search 함수를 구현하는 것이다.
만약 찾으려는 값이 배열에 존재하지 않으면 '''-1을 리턴'''한다.
동작 방식은 다음과 같다.
여기서는 중복된 값이 일치하는 경우에 대해서는 아무 인덱스나 출력하면 되는 것으로 가정한다.
@@ -23,10 +23,10 @@
1. 배열의 중앙에 위치한 값을 pivot으로 잡는다.
2. 찾으려는 값과 pivot에 위치한 값을 비교한다.
2-1. 만약 그 값이 일치한다면, 찾은 것이다.
3-1. pivot을 포함해 그 이후의 부분들은 무조건 찾으려는 값보다 크므로 검색 대상에서 제외한다.
5. 남은 부분의 배열에서 중간에 위치한 값을 pivot으로 잡고 2로 이동한다.
}}}
2. 찾으려는 값과 pivot에 위치한 값을 비교한다.
2-1. 만약 그 값이 일치한다면, 찾은 것이다.
2-2. 만약 그 값이 pivot에 위치한 값보다 크면 3-1로 이동한다.
2-2. 만약 그 값이 pivot에 위치한 값보다 작으면 3-1로 이동한다.
2-3. 만약 그 값이 pivot에 위치한 값보다 크면 3-2로 이동한다.3-1. pivot을 포함해 그 이후의 부분들은 무조건 찾으려는 값보다 크므로 검색 대상에서 제외한다.
3-2. pivot을 포함해 그 이전의 부분들은 무조건 찾으려는 값보다 크므로 검색 대상에서 제외한다.
3-2. pivot을 포함해 그 이전의 부분들은 무조건 찾으려는 값보다 작으므로 검색 대상에서 제외한다.
4. 만약 더 이상 제외할 수 없다면(최근의 검사 대상이 마지막 검색 대상이었다면) 이 배열에는 찾으려는 값이 없으므로 알고리즘을 종료한다.5. 남은 부분의 배열에서 중간에 위치한 값을 pivot으로 잡고 2로 이동한다.
}}}
@@ -79,7 +79,16 @@
}
}}}
== Depth-First Search ==
----
-----------------------------------
}}}
== Depth-First Search ==
''문제''
'''문제'''
Depth-First Search는 트리 구조에 적용되는 검색 알고리즘이다.
두 번째 과제는 깊이-우선 탐색을 이용해서 '''이진 트리'''를 순회하여 원하는 값의 존재유무를 검색하여 위치를 출력하는 depth_first_search를 구현하는 것이다.
만약 찾으려는 값이 존재하지 않으면 '''-1을 리턴'''한다.
|| attachment:300px-Depth-first-tree.png || attachment:192px-Binary_tree.png ||
|| ''깊이-우선 탐색의 검색 순서'' || '''''이진 트리''''' ||
|| ''위 사진은 '''이진 트리'''가 아님'' || 사진 : http://en.wikipedia.org/ ||
그런데, 우리는 1차원 배열을 논리적으로 2진 트리처럼 생각할 수 있다. 그 방법은 다음과 같다.
----
-----------------------------------
1. 예고 ¶
요구사항 : 지금까지 배운 내용을 모두 알고 있어야 함
출제방식 : 새로운 개념을 이용하는 프로그램을 만든다
보상 : 테스트 실패시 보강 진행
출제방식 : 새로운 개념을 이용하는 프로그램을 만든다
보상 : 테스트 실패시 보강 진행
| 문제 | 종류 | 난이도 |
| 1단계 | Binary Search | 보통 |
| 2단계 | BFS / DFS 중 하나 출제 | 어려움 |
| 3단계 | Bayesian Classifier | 지옥불 |
2.1. Binary Search ¶
문제
binary search(이진 탐색)는 이미 정렬된 배열을 대상으로 수행하는 검색 알고리즘이다.
첫 번째 과제는 오름차순으로 정렬된 정숫값을 가지는 1차원 배열로부터 원하는 값의 존재유무를 검색하여 인덱스 번호를 출력하는 binary_search 함수를 구현하는 것이다.
만약 찾으려는 값이 배열에 존재하지 않으면 -1을 리턴한다.
binary search(이진 탐색)는 이미 정렬된 배열을 대상으로 수행하는 검색 알고리즘이다.
첫 번째 과제는 오름차순으로 정렬된 정숫값을 가지는 1차원 배열로부터 원하는 값의 존재유무를 검색하여 인덱스 번호를 출력하는 binary_search 함수를 구현하는 것이다.
만약 찾으려는 값이 배열에 존재하지 않으면 -1을 리턴한다.
동작 방식은 다음과 같다.
여기서는 중복된 값이 일치하는 경우에 대해서는 아무 인덱스나 출력하면 되는 것으로 가정한다.
여기서는 중복된 값이 일치하는 경우에 대해서는 아무 인덱스나 출력하면 되는 것으로 가정한다.
1. 배열의 중앙에 위치한 값을 pivot으로 잡는다. 2. 찾으려는 값과 pivot에 위치한 값을 비교한다. 2-1. 만약 그 값이 일치한다면, 찾은 것이다. 2-2. 만약 그 값이 pivot에 위치한 값보다 작으면 3-1로 이동한다. 2-3. 만약 그 값이 pivot에 위치한 값보다 크면 3-2로 이동한다. 3-1. pivot을 포함해 그 이후의 부분들은 무조건 찾으려는 값보다 크므로 검색 대상에서 제외한다. 3-2. pivot을 포함해 그 이전의 부분들은 무조건 찾으려는 값보다 작으므로 검색 대상에서 제외한다. 4. 만약 더 이상 제외할 수 없다면(최근의 검사 대상이 마지막 검색 대상이었다면) 이 배열에는 찾으려는 값이 없으므로 알고리즘을 종료한다. 5. 남은 부분의 배열에서 중간에 위치한 값을 pivot으로 잡고 2로 이동한다.
함수 정의 예시는 다음과 같다.
int binary_search(int* arr, int tofind, int start, int end) {
int pivot = [start와 end의 중간];
/* 주요부분 생략 */
if (end < start) return -1;
return binary_search(arr, tofind, start, end);
}
테스트용 코드
#include <stdio.h>
#pragma warning(disable:4996)
int binary_search(int*, int, int, int); //function prototype
int main(void) {
int arr1[10] = { 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 };
int arr2[10] = { 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 };
int arr3[10] = { 5, 5, 5, 10, 10, 10, 10, 15, 15, 15 };
for (int i = 0; i < 10; i++) {
printf("%d ", arr1[i]);
}
printf("\n\n===================\n\n");
for (int i = 0; i < 10; i++) {
printf("%d ", arr2[i]);
}
printf("\n\n===================\n\n");
for (int i = 0; i < 10; i++) {
printf("%d ", arr3[i]);
}
printf("\n\n===================\n\n");
int scan;
printf("Input number to find : ");
scanf("%d", &scan);
printf("Input number found at %d, %d, %d", binary_search(arr1, scan, 0, 9), binary_search(arr2, scan, 0, 9), binary_search(arr3, scan, 0, 9));
return 0;
}
2.2. Depth-First Search ¶
문제
Depth-First Search는 트리 구조에 적용되는 검색 알고리즘이다.
두 번째 과제는 깊이-우선 탐색을 이용해서 이진 트리를 순회하여 원하는 값의 존재유무를 검색하여 위치를 출력하는 depth_first_search를 구현하는 것이다.
만약 찾으려는 값이 존재하지 않으면 -1을 리턴한다.
그런데, 우리는 1차원 배열을 논리적으로 2진 트리처럼 생각할 수 있다. 그 방법은 다음과 같다.
Depth-First Search는 트리 구조에 적용되는 검색 알고리즘이다.
두 번째 과제는 깊이-우선 탐색을 이용해서 이진 트리를 순회하여 원하는 값의 존재유무를 검색하여 위치를 출력하는 depth_first_search를 구현하는 것이다.
만약 찾으려는 값이 존재하지 않으면 -1을 리턴한다.
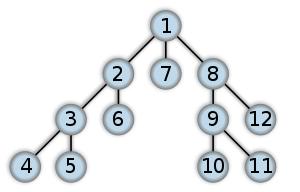 [PNG image (35.97 KB)] | 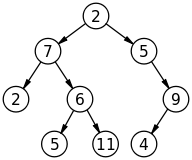 [PNG image (6.09 KB)] |
| 깊이-우선 탐색의 검색 순서 | 이진 트리 |
| 위 사진은 이진 트리가 아님 | 사진 : http://en.wikipedia.org/ |
그런데, 우리는 1차원 배열을 논리적으로 2진 트리처럼 생각할 수 있다. 그 방법은 다음과 같다.










