Difference between r1.13 and the current
@@ -7,13 +7,12 @@
* Hash Table(간략하게, Tree 위주. Associative array를 설명할 때 필요는 하므로.)
= 참여자 =
||강사 || [권영기] ||
|| ||
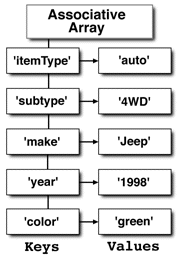
== Associative array ==
* In computer science, an associative array, map, symbol table, or dictionary is an abstract data type composed of a collection of (key, value) pairs, such that each possible key appears at most once in the collection.
= 참여자 =
||강사 || [권영기] ||
||<|10> 참여자|| ||
|| ||
|| ||
|| ||
|| [] ||
|| [] ||
||<|10> 참여자|| [김정민] ||
|| [이지수] ||
|| [최다인] ||
|| [성훈] ||
|| [이태균] ||
|| [이원준] ||
= 내용 === Associative array ==
* In computer science, an associative array, map, symbol table, or dictionary is an abstract data type composed of a collection of (key, value) pairs, such that each possible key appears at most once in the collection.
@@ -66,12 +65,49 @@
printCarInfo(carinfo);
}
}}}
[새싹교실/2014], [새싹교실/2014/다빈치인재반]
}
}}}
* [http://www.cplusplus.com/reference/map/map/]
* [http://www.hanbit.co.kr/network/view.html?bi_id=1618]
attachment:result.PNG
=== Implementation ===
* Hash Table
* Binary Search Tree
== Binary Search Tree ==
* [http://www.cs.cmu.edu/~adamchik/15-121/lectures/Trees/trees.html]
=== Visualization ===
* [https://www.cs.usfca.edu/~galles/visualization/BST.html]
== Indexed Binary Search Tree ==
* Binary search tree
* Each node has an additional field.
* leftsize = number of nodes in its left subtree
attachment:sample.png
=== Why we use indexed binary search tree? ===
* Index를 이용해서 값을 검색, 삽입, 삭제, 수정이 가능하다.
* 여기서 Index는 Rank와 같은 개념이라고 생각하자. Tree 내부의 Element의 Inorder 순서의 위치라고 생각할 수 있다.
* Inorder 순서의 위치?
* Binary Search Tree에서 Inorder를 수행할 경우, key 값이 오름차순으로(혹은 내림차순으로) 노드들을 탐색한 결과가 나올 것이다.
* 다시 말해서, Index는 Tree에 내부의 Element가 몇 번째로 작은지(혹은 큰지)를 가리키는 것이 된다.
* 기존의 Binary Search Tree 만으로 위와 같은 수행을 하기 위해서는 모든 노드를 살펴보는 수 밖에 없다.
=== Operation ===
* Search(index)
* Delete(index)
* Insert(index, value)
* 여기서 핵심은 어떻게 주어진 index로 트리의 노드를 접근하는가이다.
* if index = x.leftSize desired element is x.element
* if index < x.leftSize desired element is index’th element in left subtree of x
* if index > x.leftSize desired element is (index - x.leftSize-1)’th element in right subtree of x
* 나머지 Delete를 어떻게 할 것이냐, Insert를 어떻게 할 것이냐는 Binary Search Tree와 같으므로 생략.
== Hash Table ==
* http://sweeper.egloos.com/viewer/925740
= 후기 = * 막상 후기를 쓰려니 너무 오래되서 별로 생각이 안나지만... 위키 내용을 보며 기억을 떠올려 보니, 인덱시드 바이너리 서치 트리에서 leftsize를 이용하는 부분이 굉장히 인상깊었던게 떠오르네요. 과제를 하면서 내용을 되새겼어야 되는데... 과제를 안해서 기억이 잘 안나는게 아쉽군요. 다음부턴 과제에 시간 좀 할애해야 할 듯 합니다. - [김정민]
= 숙제 = * Binary Search Tree 구현 (시간 남으면 Indexed도 구현)
= 참조 =
* Associative array : [http://en.wikipedia.org/wiki/Associative_array]
* map : [http://www.cplusplus.com/reference/map/map/]
* map : [http://www.hanbit.co.kr/network/view.html?bi_id=1618]
* Binary Search Tree : [http://www.cs.cmu.edu/~adamchik/15-121/lectures/Trees/trees.html]
* Binary Search Tree Visualization : [https://www.cs.usfca.edu/~galles/visualization/BST.html]
* Indexed Binary Search Tree : 2013년 한상용 교수님 자료구조 5-4 BinarySearchTree ppt
* Hash Table : [http://sweeper.egloos.com/viewer/925740]
----[새싹교실/2014], [새싹교실/2014/다빈치인재반]
1. 계획 ¶
- Associative array
- Maps in STL
* JSON
- Binary Search Tree
- Hash Table(간략하게, Tree 위주. Associative array를 설명할 때 필요는 하므로.)
3.1. Associative array ¶
- In computer science, an associative array, map, symbol table, or dictionary is an abstract data type composed of a collection of (key, value) pairs, such that each possible key appears at most once in the collection.
- In an associative array, the association between a key and a value is often known as a "binding", and the same word "binding" may also be used to refer to the process of creating a new association.
3.1.1. Operations ¶
- Add or insert: add a new (key, value) pair to the collection, binding the new key to its new value. The arguments to this operation are the key and the value.
- Reassign: replace the value in one of the (key, value) pairs that are already in the collection, binding an old key to a new value. As with an insertion, the arguments to this operation are the key and the value.
- Remove or delete: remove a (key, value) pair from the collection, unbinding a given key from its value. The argument to this operation is the key.
- Lookup: find the value (if any) that is bound to a given key. The argument to this operation is the key, and the value is returned from the operation. If no value is found, some associative array implementations raise an exception.
3.1.2.1. C++ ¶
#include<iostream>
#include<string>
#include<map>
using namespace std;
void printCarInfo(map <string,string> &carinfo){
cout<<"----------------------------------------------"<<endl;
map <string, string>::iterator it1;
for(it1 = carinfo.begin(); it1 != carinfo.end(); it1++){
cout<<it1->first<<" : "<<it1->second<<endl;
}
}
int main(void){
map <string, string> carinfo;
carinfo.insert(map<string, string>::value_type("itemType", "auto"));
carinfo.insert(make_pair("subtype", "4WD"));
carinfo["make"] = "Jeep";
carinfo["year"] = "1998";
carinfo["color"] = "green";
//Insert Key-Value Pair
printCarInfo(carinfo);
map <string, string>::iterator FindIter = carinfo.find("year");
if(FindIter != carinfo.end()){
FindIter->second = "2002";
}
//Lookup & Reassign
printCarInfo(carinfo);
carinfo["year"] = "2013";
//Reassign
printCarInfo(carinfo);
carinfo.erase("year");
//delete
printCarInfo(carinfo);
}
[PNG image (25.48 KB)]
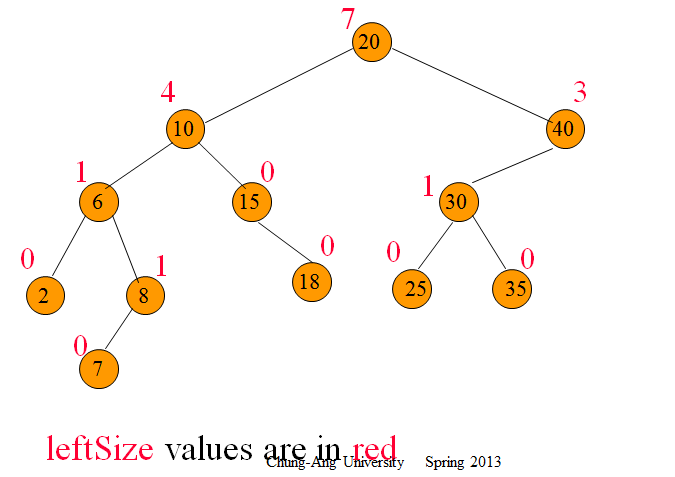
3.3. Indexed Binary Search Tree ¶
- Binary search tree
- Each node has an additional field.
- leftsize = number of nodes in its left subtree
 [PNG image (20.88 KB)]
[PNG image (20.88 KB)]
- leftsize = number of nodes in its left subtree
3.3.1. Why we use indexed binary search tree? ¶
- Index를 이용해서 값을 검색, 삽입, 삭제, 수정이 가능하다.
- 여기서 Index는 Rank와 같은 개념이라고 생각하자. Tree 내부의 Element의 Inorder 순서의 위치라고 생각할 수 있다.
- Inorder 순서의 위치?
- Binary Search Tree에서 Inorder를 수행할 경우, key 값이 오름차순으로(혹은 내림차순으로) 노드들을 탐색한 결과가 나올 것이다.
- Binary Search Tree에서 Inorder를 수행할 경우, key 값이 오름차순으로(혹은 내림차순으로) 노드들을 탐색한 결과가 나올 것이다.
- 다시 말해서, Index는 Tree에 내부의 Element가 몇 번째로 작은지(혹은 큰지)를 가리키는 것이 된다.
- Inorder 순서의 위치?
- 기존의 Binary Search Tree 만으로 위와 같은 수행을 하기 위해서는 모든 노드를 살펴보는 수 밖에 없다.
3.3.2. Operation ¶
- Search(index)
- Delete(index)
- Insert(index, value)
- 여기서 핵심은 어떻게 주어진 index로 트리의 노드를 접근하는가이다.
- if index = x.leftSize desired element is x.element
- if index < x.leftSize desired element is index’th element in left subtree of x
- if index > x.leftSize desired element is (index - x.leftSize-1)’th element in right subtree of x
- 나머지 Delete를 어떻게 할 것이냐, Insert를 어떻게 할 것이냐는 Binary Search Tree와 같으므로 생략.
4. 후기 ¶
- 막상 후기를 쓰려니 너무 오래되서 별로 생각이 안나지만... 위키 내용을 보며 기억을 떠올려 보니, 인덱시드 바이너리 서치 트리에서 leftsize를 이용하는 부분이 굉장히 인상깊었던게 떠오르네요. 과제를 하면서 내용을 되새겼어야 되는데... 과제를 안해서 기억이 잘 안나는게 아쉽군요. 다음부턴 과제에 시간 좀 할애해야 할 듯 합니다. - 김정민
6. 참조 ¶
- Associative array : http://en.wikipedia.org/wiki/Associative_array
- map : http://www.cplusplus.com/reference/map/map/
- map : http://www.hanbit.co.kr/network/view.html?bi_id=1618
- Binary Search Tree : http://www.cs.cmu.edu/~adamchik/15-121/lectures/Trees/trees.html
- Binary Search Tree Visualization : https://www.cs.usfca.edu/~galles/visualization/BST.html
- Indexed Binary Search Tree : 2013년 한상용 교수님 자료구조 5-4 BinarySearchTree ppt
- Hash Table : http://sweeper.egloos.com/viewer/925740